H26年度 神奈川県立高校の入試問題解説 数学の問3(イ)(ウ)です。
数学 問3 (イ)
一次関数の基本形
\(y=mx+n\)
\(m\)は変化の割合(傾き)
\(n\)は\(y\)切片
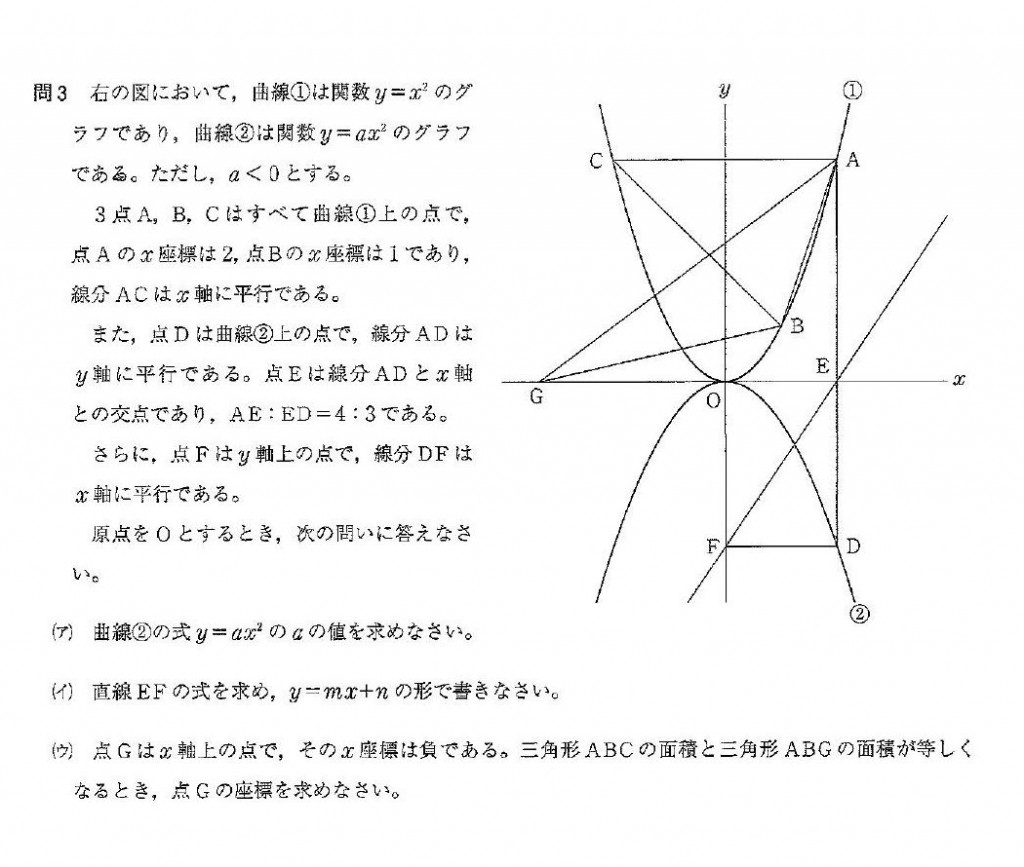
(ア)で導き出したように、直線EFの\(y\)切片Fの座標は\((0,―3)\)となります。
したがって、\(y=mx+n\) の\(n\)に―3を代入。
\(y=mx-3\)
これに点E\((2,0)\)を代入します。 ⇔ \(x=2,y=0\) を代入。
\(0=2m-3\)
\(-2m=-3\)
\(\displaystyle m=\frac{-3}{-2}\)
\(\displaystyle m=\frac{3}{2}\)
\(\displaystyle ∴\ \ y=\frac{3}{2}x-3\)
別解
\(y\)切片は―3を利用して、傾きをグラフから求めます。
\(\displaystyle 傾き(変化の割合)=\frac{yの増加量}{xの増加量}\) を利用して、
\(\displaystyle m=\frac{3}{2}\)
数学 問3 (ウ)
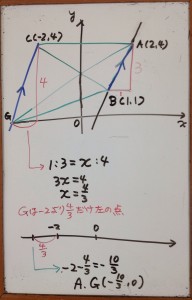
△ABCと△ABGの面積が等しくなるように、等積変形で考えます。
底辺に平行な直線上のどこに頂点を置いても、底辺と高さが等しいので面積も等しくなります。
等積変形の問題のポイント
共通している辺を底辺として、頂点を通り底辺に平行な直線を引く!
平行な2つの直線の傾きは等しい!
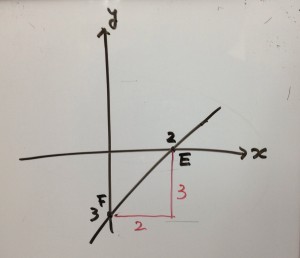
△ABCと△ABGで共通している辺は辺ABですから、点Cを通り辺ABに平行な直線を引きます。
この直線と\(x\)軸との交点が、求める点Gとなります。
では、直線CGの式を求めましょう。
直線ABと直線CGは平行なので傾きは等しくなります。
直線ABの\(\displaystyle 傾き=\frac{4-1}{2-1}=3\) ……① となり、直線CGの傾きも3となります。
したがって、直線CGの式を \(y=3x+b\)とおいて、点Cを代入します。
線分ACは\(x\)軸に平行なので、点Aと点Cは\(y\)軸に対して線対称となります。
(\(y\)軸に対して対称⇔\(x\)座標は符号が逆、\(y\)座標は等しい)
点Cの座標は \((-2,4)\) となるので、これを①に代入します。
\(4=3\times(-2)+b\)
\(-4=-6+b\)
\(-b=-6+4\)
\(-b=-10\)
\(b=10\)
∴ 直線CG:\(y=3x+10\)……②
点Gは\(x\)軸との交点なので、\(y\)座標\(=0\)
②に\(y=0\)を代入して、
\(~~~0=3x+10\)
\(-3x=10\)
\(\displaystyle ~~~x=-\frac{10}{3}\)
∴ 点G \(\displaystyle (-\frac{10}{3},0)\)
別解
AB//CG を 利用して相似な三角形から 比で求めます。
H26年度 神奈川県立高校 数学入試問題解説
H26年度 神奈川県立高校 数学入試問題解説 問1
H26年度 神奈川県立高校 数学入試問題解説 問2
H26年度 神奈川県立高校 数学入試問題解説 問3(ア)
H26年度 神奈川県立高校 数学入試問題解説 問3(イ)(ウ)


コメント
[…] 解説のページでさっそく使ってます! H26年度 神奈川県立高校 数学入試問題解説 問3(イ)(ウ) […]