中学1年生の数学の解説です。
数学の解き方 で 解説した「3つの要素」を 意識しましょう。
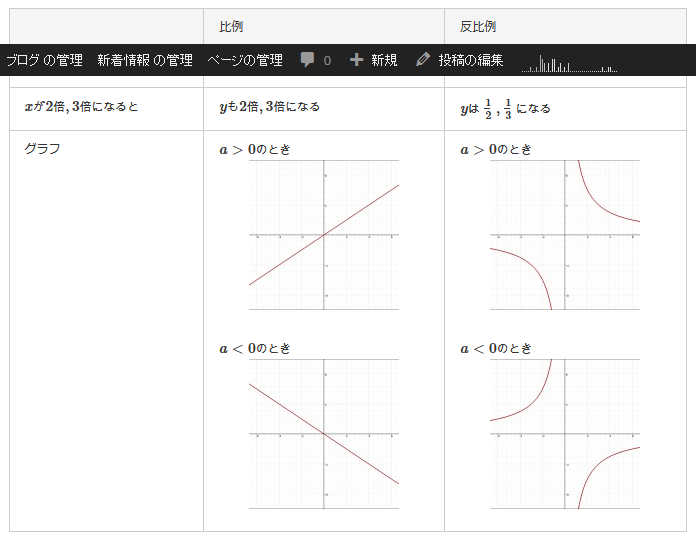
比例・反比例 どちらも \(x,y,a\) の 3つの要素があります。
\(x,y\)を 与えられるので、残りの \(a\) を 求めましょう。
比例の式:\(y=ax\) と 反比例の式:\(\displaystyle y=\frac{a}{x}\) の比例定数(\(a\)の部分)を求めましょう。
※ まず「解法:1」で、座標(x,yの値)を代入して解くという、関数の基本について理解してください。これが理解できずに、公式として「解法:2」だけを暗記すると、今後出てくる1次関数や2次関数でつまづきます。「解法:1」が理解できたら「解法:2」の練習を繰り返して、比例定数を暗算で瞬間に計算できるように練習しましょう! (暗算で計算できても”式”は書くこと!)
比例の問題
\(yがxに比例して、x=3のときy=9となる。yをxの式で表しなさい。\)
- \(y\)が\(x\)に比例するので、\(y=ax\)の式を使います。
- \(y,a,x\)の3つの文字のうち、\(x\)と\(y\)については分かったので、代入して\(a\)を求めます。
解法:1…基本的な解法を理解しよう!
\(y=axに x=3,y=9を代入\)
\(9=3a\)
\((3a=9:左辺にaがくるように両辺を入れ替え)\)
\(\displaystyle a=\frac{9}{3}\)
\(a=3\)
\(∴ y=3x\)
- \(y=ax\)より、\(\displaystyle a=\frac{y}{x}\)(両辺をxでわる)
- これを利用すれば、\(x\)を分母,\(y\)を分子に入れるだけで\(a\)が出ます。
- 【注意】約分を忘れない!
解法:2…基本が理解できたら、比例定数を簡単に求めよう!
\(\displaystyle a=\frac{9}{3}\)
\(a=3\)
\(∴ y=3x\)
反比例の問題
\(yがxに反比例して、x=2のときy=3となる。yをxの式で表しなさい。\)
- \(y\)が\(x\)に反比例するので、\(y=\frac{a}{x}\)の式を使います。
- \(y,a,x\)の3つの文字のうち、\(x\)と\(y\)については分かったので、代入して\(a\)を求めます。
解法:1…基本的な解法を理解しよう!
\(\displaystyle y=\frac{a}{x}に x=2,y=3を代入\)
\(\displaystyle 3=\frac{a}{2}\)
\(\displaystyle (\frac{a}{2}=3:左辺にaがくるように両辺を入れ替え)\)
\(a=3\times2\)
\(a=6\)
\(\displaystyle ∴ y=\frac{6}{x}\)
- \(\displaystyle y=\frac{a}{x}\)より、\(a=xy\)(両辺にxをかける)
- これを利用すれば、\(x\)と\(y\)をかけるだけで\(a\)が出ます。
解法:2…基本が理解できたら、比例定数を簡単に求めよう!
\(a=2\times3\)
\(a=6\)
\(\displaystyle ∴ y=\frac{6}{x}\)
しっかりとマスターしてくださいね!
比例と反比例のほかの記事
比例と反比例 1:式とグラフ

コメント
[…] 比例と反比例 2:式を求める […]
[…] 比例と反比例 2:式を求める […]
[…] 中学1年の数学 「比例と反比例 2:式を求める」の練習問題です。 […]