今回は、神奈川県立高校入試問題より、問6について解説を掲載します。
解法についても複数あります。
内容としては基本的な問題ですが、解法の選択でかかる時間が大きく変わってきます。
単元にとらわれずに柔軟に発想できることが、より早く正確に解ける近道です。
柔軟な発想の根底に流れるものは、いつでも取り出せる各単元の基礎力です。
特に(イ)では、小学校の知識で解けますが、意外と三平方の問題ととらわれがちです。
入試直前だけではなく、普段からの練習での基礎力養成が不可欠です。
数学 問6 問題
>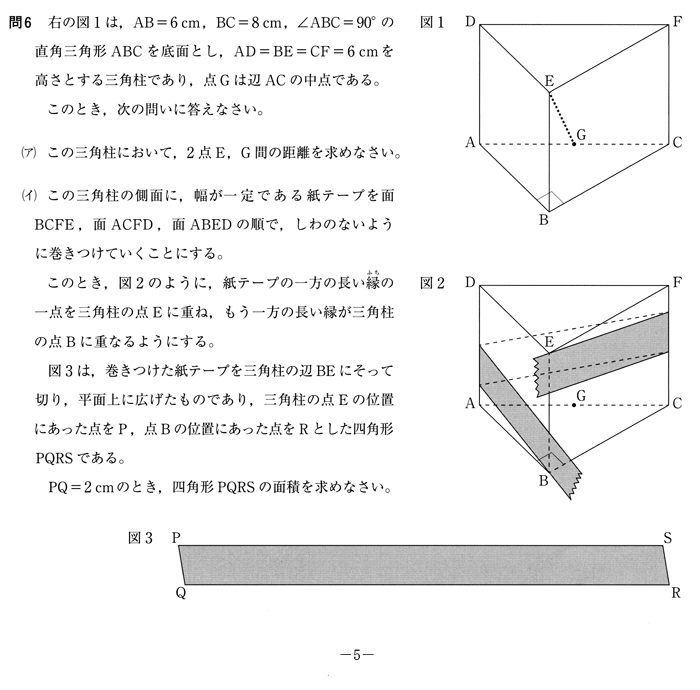
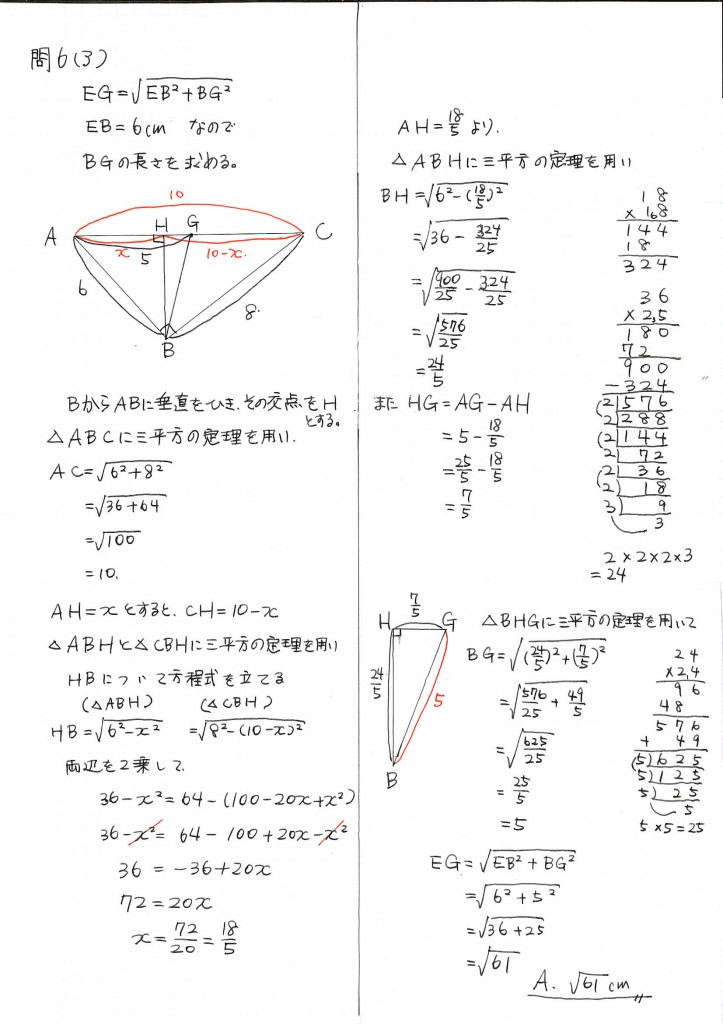
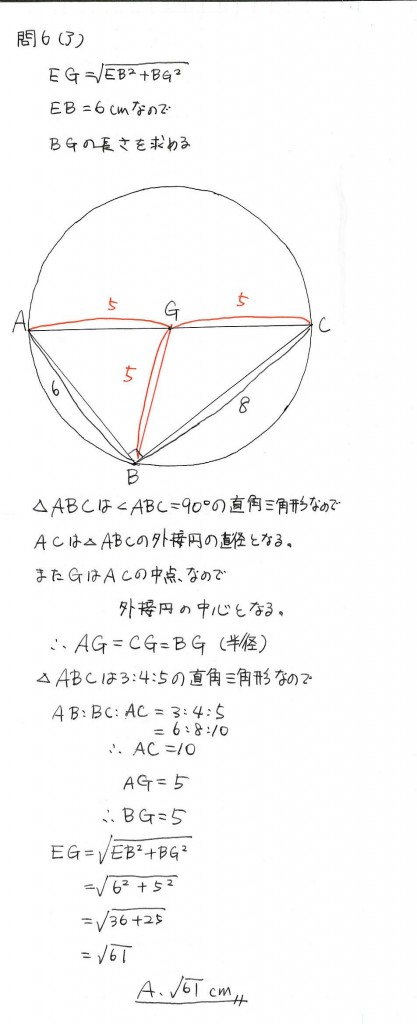
(ア)解法
空間図形に三平方の定理を用い、時間はかかりますが1つ1つ解いていきます。
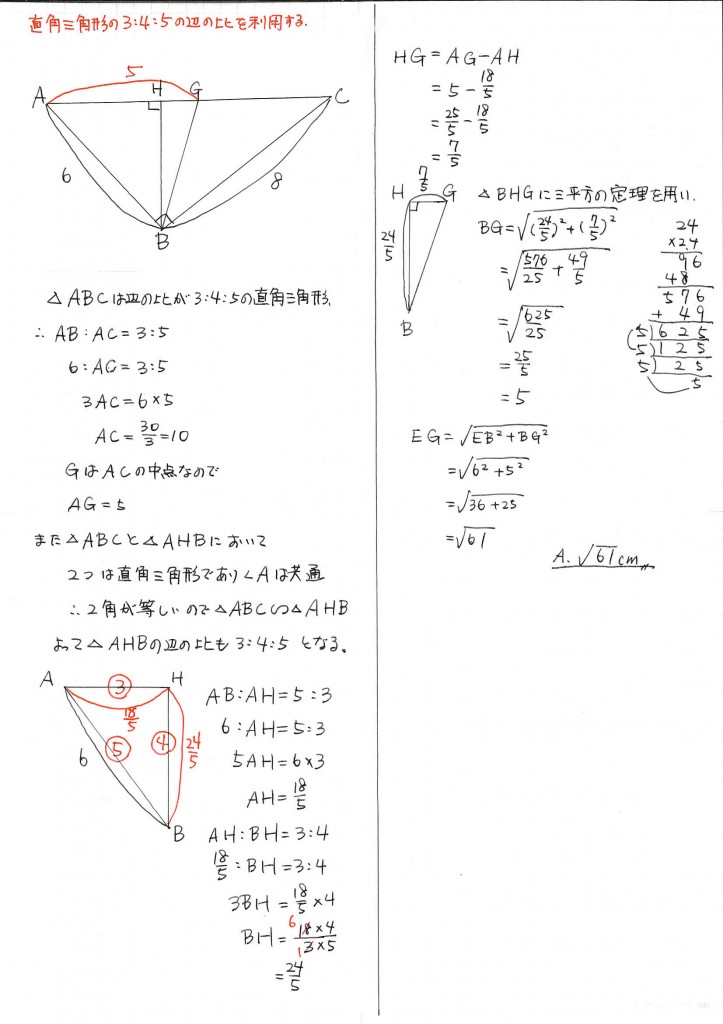
直角三角形の辺の比を利用し計算を効率的に進めます。
円と円周角の定理から、簡単に求めます。
(イ)解法
展開図より必要な部分の長さを三平方の定理で求めます。

小学校の面積の問題の基礎力で解きます。
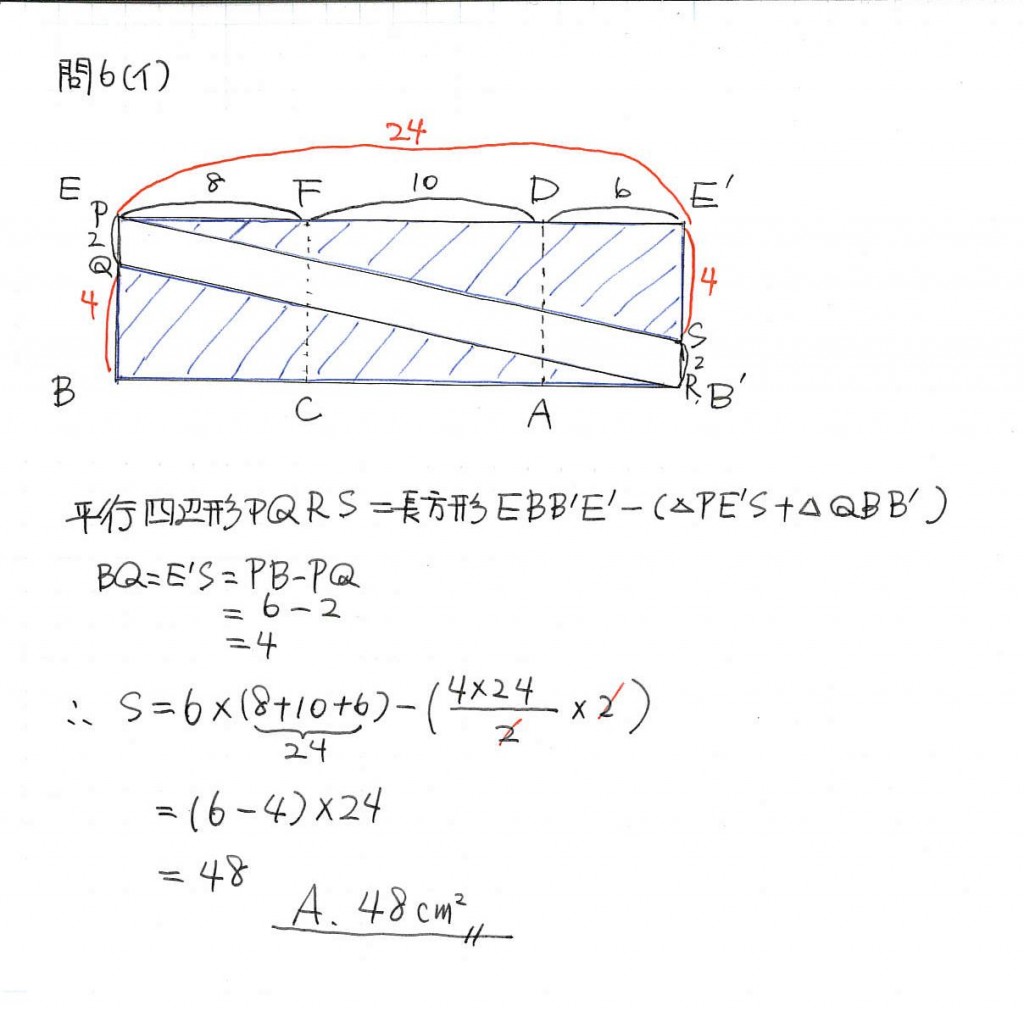
更に平行四辺形PQRSは底辺PQ、高さPE’と考えて
2×24=48 として求めることもできます。